
Some mathematicians have sought a logical proof for the existence of God. Here’s what they discovered
By Manon Bischoff
Who would have thought about God as an apt topic for an essay about mathematics? Don’t worry, the following discussion is still solidly grounded within an intelligible scientific framework. But the question of whether God can be proved mathematically is intriguing. In fact, over the centuries, several mathematicians have repeatedly tried to prove the existence of a divine being. They range from Blaise Pascal and René Descartes (in the 17th century) to Gottfried Wilhelm Leibniz (in the 18th century) to Kurt Gödel (in the 20th century), whose writings on the subject were published as recently as 1987. And probably the most amazing thing: in a preprint study first posted in 2013 an algorithmic proof wizard checked Gödel’s logical chain of reasoning—and found it to be undoubtedly correct. Has mathematics now finally disproved the claims of all atheists?
As you probably already suspect, it has not. Gödel was indeed able to prove that the existence of something, which he defined as divine, necessarily follows from certain assumptions. But whether these assumptions are justified can be called into doubt. For example, if I assume that all cats are tricolored and know that tricolored cats are almost always female, then I can conclude: almost all cats are female. Even if the logical reasoning is correct, this of course does not hold. For the very assumption that all cats are tricolored is false. If one makes statements about observable things in our environment, such as cats, one can verify them by scientific investigations. But if it is about the proof of a divine existence, the matter becomes a little more complicated.
While Leibniz, Descartes and Gödel relied on an ontological proof of God in which they deduced the existence of a divine being from the mere possibility of it by logical inference, Pascal (1623–1662) chose a slightly different approach: he analyzed the problem from the point of view of what might be considered today as game theory and developed the so-called Pascal’s wager.
To do this, he considered two possibilities. First, God exists. Second, God does not exist. Then he examined the consequences of believing or not believing in God after death. If there is a divine being, and one believes in it, one ends up in paradise; otherwise one goes to hell. If, on the other hand, there is no God, nothing else happens—regardless of whether you are religious or not. The best strategy, Pascal contends, is to believe in God. At best, you end up in paradise; in the worst scenario, nothing happens at all. If, on the other hand, you don’t believe, then in the worst case you could end up in hell.
Pascal’s thoughts are comprehensible—but they refer to scenarios from religious writings and do not represent a proof for the existence of a superior being. They only say that one should join the faith based on opportunism.
Ontological approaches dealing with the nature of being are more convincing, even if they will most likely not change the minds of atheists. Theologian and philosopher Anselm of Canterbury (1033–1109) put forward his ideas at the beginning of the last millennium. He described God as a being beyond whom nothing greater can be thought. But if God does not exist, then one can imagine something greater: namely, a being beyond which nothing greater can be contemplated. But like God, this being also exists and exhibits a property of ultimate greatness. This, of course, is absurd: nothing can be greater than the greatest thing that one can imagine. Accordingly, the assumption that God does not exist must be wrong.
It took a few centuries for this idea to be revisited—by none other than Descartes (1596–1650). Supposedly unaware of Anselm’s writings, he provided an almost identical argument for the divine existence of a perfect being. Leibniz (1646–1716) took up the work a few decades later and found fault with it: Descartes, he contended, had not shown that the “perfect properties” of certain entities, ranging from triangles to God, are compatible. Leibniz went on to argue that perfection could not be properly investigated. Therefore, it could never be disproved that perfect properties unite in one being. Thus, the possibility of a divine being must be real. So based on Anselm’s and Descartes’s arguments, it necessarily follows that God exists.
From a mathematical point of view, however, these thought experiments became really serious only through Gödel’s efforts. This is not too surprising: The scientist had already turned the subject on its head at the age of 25 by showing that mathematics always contains true statements that cannot be proved. In doing so, he made use of logic. This same logic also enabled him to prove the existence of God. Take a look at these 12 steps made up of a set of axioms (Ax), theorems (Th) and definitions (Df).
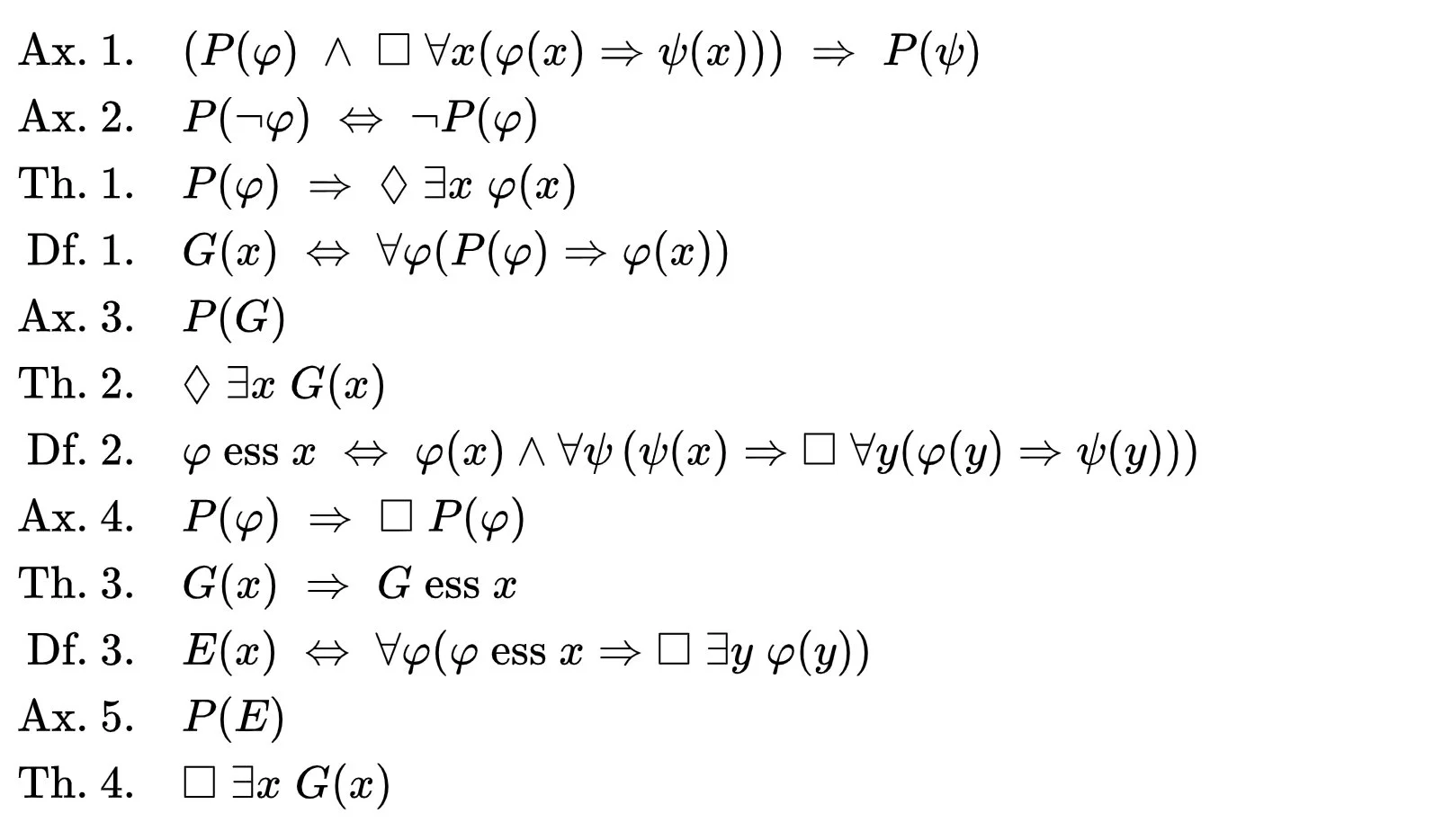
At first glance, they seem cryptic, but one can go through them step by step to follow Gödel’s thinking. He starts with an axiom—an assumption, in other words: If φ has the property P and from φ always follows ψ, then ψ also has the property P. For simplicity, we can assume that P stands for “positive”. For example:, if a fruit is delicious, a positive property, then it is also fun to eat. Therefore, the fun of eating it is also a positive property.
The second axiom further sets a framework for P. If the opposite of something is positive, then that “something” must be negative. Thus, Gödel has divided a world into black and white: Either something is good or bad. For example, if health is good, then a disease must necessarily be bad.
With these two premises, Gödel can derive his first theorem: If φ is a positive property, then there is a possibility that an x with property φ exists. That is, it is possible for positive things to exist.
Now the mathematician turns for the first time to the definition of a divine being: x is divine if it possesses all positive properties φ. The second axiom ensures that a God defined in this way cannot have negative characteristics (otherwise one would create a contradiction).
The third axiom states that divinity is a positive characteristic. This point is not really arguable because divinity combines all positive characteristics.
The second theorem now becomes a bit more concrete: by combining the third axiom (divinity is positive) and the first theorem (there is the possibility that something positive exists), a being x could exist that is divine.
Gödel’s goal now is to show in the following steps that God must necessarily exist in the framework that has been laid out. For this purpose, he introduces in the second definition the “essence” φ of an object x, a characteristic property that determines all other characteristics. An illustrative example is “puppylike if something has this property, it is necessarily cute, fluffy and clumsy.
The fourth axiom doesn’t seem too exciting at first. It simply states that if something is positive, then it is always positive—no matter the time, situation or place. Being puppylike and tasting good, for example, are always positive, whether during the day or at night in Heidelberg, Germany, or Buenos Aires.
Gödel can now formulate the third theorem: if a being x is divine, then divinity is its essential property. This makes sense because if something is divine, it possesses all positive characteristics—and thus the properties of x are fixed.
The next step relates to the existence of a particular being. If somewhere at least one being y possesses the property φ, which is the essential property of x, then x also exists. That is, if anything is puppy-like, then puppies must also exist.
According to the fifth axiom, existence is a positive property. I think most people would agree with that.
From this one can now conclude that God exists because this being possesses every positive property, and existence is positive.
As it turns out, Gödel’s logical inferences are all correct—even computers have been able to prove that. Nevertheless, these inferences have also drawn criticism. Besides the axioms, which of course can be questioned (why should a world be divisible into “good” and “evil”?), Gödel does not give more details about what a positive property is.
It’s true that by means of the definitions and axioms, one can describe the set P mathematically:
If a property belongs to the set, its negation is not included. The set is self-contained.
The fact that the essence of the set has only the characteristics of the set is itself an element of the set. The set always has the same elements—independent of the situation. In this case, the situation is the mathematical model in which the set is contained.
Existence is part of the set.
If φ is part of the set, then the property of having φ as the essence of the set is also contained in the set.
But all of this does not ensure that this set is unique. There could be multiple collections that satisfy the requirements. For example, as logicians have shown, it is possible to construct cases where, by Gödel’s definition, there are more than 700 divine entities that differ in essence.
This does not settle the final question of the existence of one (or more) divine beings. Whether mathematics is really the right way to answer this question is itself questionable—even if thinking about it is quite exciting.
_________________
This article originally appeared in Spektrum der Wissenschaft.
Courtesy: Scientific American (Published on October 4, 2022)